(指数型极限运算法则)揭秘指数型极限公式：探索数学世界中的极限理论及应用技巧

揭秘指数型极限公式：探索数学世界中的极限理论及应用技巧

在数学的世界中，极限理论是微积分学的基础，而指数型极限公式则是极限理论中的一个重要组成部分，本文将围绕指数型极限公式展开，分析其在数学世界中的重要作用及其应用技巧。

指数型极限公式概述

指数型极限公式是指在函数中包含指数函数的极限表达式，常见的指数型极限公式有：

1、$lim_{n o infty} (1 + rac{1}{n})^n = e$

2、$lim_{x o 0} (1 + x)^{rac{1}{x}} = e$

3、$lim_{x o infty} (1 + rac{1}{x})^x = e$

这些公式在微积分学中具有极高的应用价值，是解决实际问题的重要工具。

指数型极限公式的应用技巧

1、极限换元法

在解决指数型极限问题时，换元法是一种常用的方法，通过换元，可以将复杂的极限问题转化为简单的极限问题。

问题：求 $lim_{x o infty} (1 + rac{1}{x})^{2x}$。

解答：令 $t = rac{1}{x}$，则 $x o infty$ 时，$t o 0$，原极限可转化为：

$lim_{t o 0} (1 + t)^{rac{1}{t} cdot 2} = lim_{t o 0} (1 + t)^{rac{2}{t}} = e^2$。

2、极限的乘除法则

在解决指数型极限问题时，运用乘除法则可以简化计算。

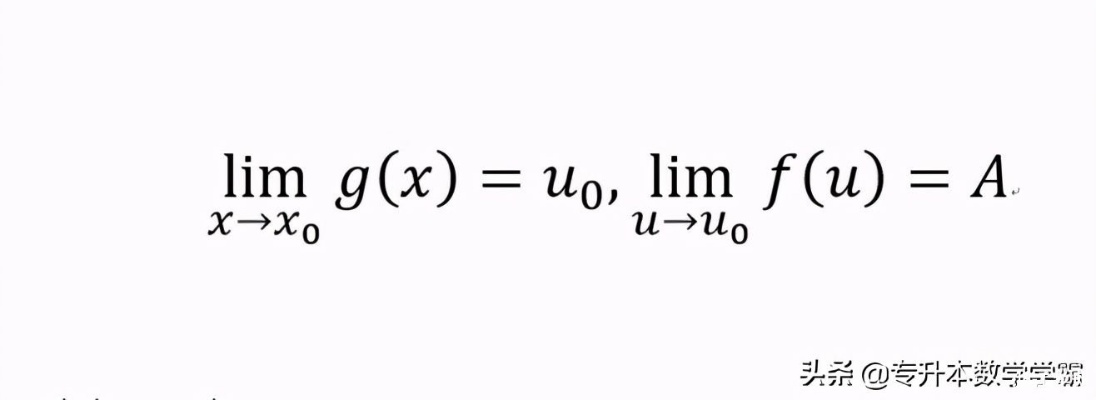
问题：求 $lim_{x o 0} (1 + 2x)^{rac{1}{x}} cdot (1 - 2x)^{rac{1}{x}}$。

解答：原极限可转化为：

$lim_{x o 0} [(1 + 2x)(1 - 2x)]^{rac{1}{x}} = lim_{x o 0} 1^{rac{1}{x}} = 1$。

常见问题解答（FAQ）

1、问：指数型极限公式有什么实际意义？

答：指数型极限公式在物理学、生物学、经济学等领域具有广泛的应用，在生物领域中，细菌的繁殖过程就可以用指数型极限公式来描述。

2、问：如何快速掌握指数型极限公式的应用技巧？

答：多做练习题，掌握常见的换元方法和乘除法则，同时要熟练掌握基本极限公式。

参考文献

1、华东师范大学数学系. 《高等数学》. 北京：高等教育出版社，2018.

2、同济大学数学系. 《高等数学》. 北京：高等教育出版社，2019.

3、数学与应用数学专业规划教材编写组. 《数学分析》. 北京：科学出版社，2017.

通过以上分析，我们可以看到指数型极限公式在数学世界中的重要作用，掌握指数型极限公式的应用技巧，有助于我们在解决实际问题时更加得心应手，了解指数型极限公式的背景和意义，也能让我们更加深入地理解数学的内涵。